REPASO TERCER PARCIAL

FORMULARIO TERCER PARCIAL

Regresión Lineal Múltiple

Mediante un modelo de regresión lineal múltiple, se pretende explicar el comportamiento de una determinada variable que denominaremos variable a explicar, variable endógena o variable dependiente, (y representaremos con la letra Y) en función de un conjunto de k variables independientes explicativas X1, X2, ..., Xk

Para determinar el modelo anterior, es necesario hallar (estimar) el valor de los coeficientes a, b1, b2, b3,.., bn.  Para encontrar una ecuación que permita estimar el valor de la variable dependiente con base en la variable independiente

Ejemplo: 

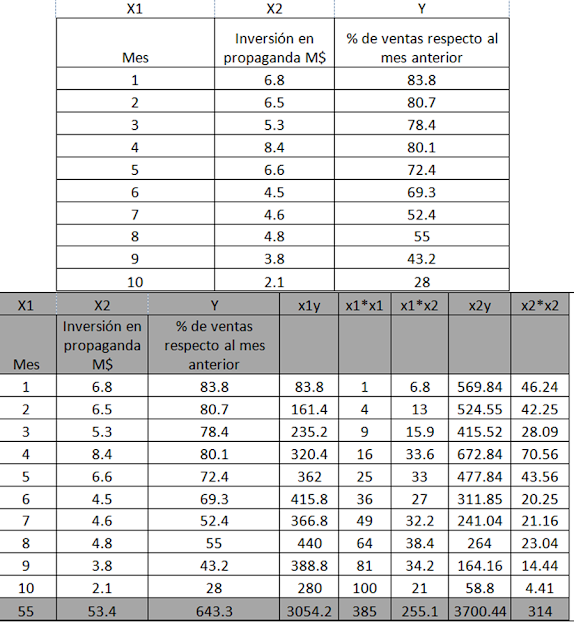
Los siguientes datos corresponden al % de ventas esperado respecto al mes anterior cuyos valores dependen tanto del mes anterior como de la inversión en propaganda.

a) Obtenga la ecuación de regresión múltiple

b) Cuál es el valor esperado para el mes 11, si la inversión en propaganda será de 2M$?

CON EXCEL 

Ejercicio de clase:

En un cierto país, se tienen los datos de ña remuneración media por hora y la tasa de desempleo entre  los años 2010 y 2014.

Remuneración por hora (Dlls)	Tasa de desempleo (%) X1	Tiempo (años) X2
2.19	6.1	2010 (1)
2.26	6.2	2011 (2)
2.32	7.8	2012 (3)
2.39	5.8	2013 (4)
2.46	5.7	2014 (5)

Obtenga:

a) La ecuación de regresión múltiple

b) Calcule la remuneración esperada para 2017, con una tasa de desempleo de 0.5

c) Calcule la remuneración esperada para 2016, con una tasa de desempleo de 5

ANÁLISIS DE REGRESIÓN LINEAL

Una vez determinada la existencia de la relación entre dos variables se procede a realizar un análisis de regresión, que consiste en:

Desarrollar la ecuación de regresión y proporcionar estimados de Y con base en valores de X, mediante el uso del Método de Mínimos Cuadrados.

La fórmula es:

Ejercicio de Tarea

La siguiente tabla muestra la tensión arterial de una muestra de pacientes de acuerdo a su edad. 

Obtenga

a)    El diagrama de dispersión

b)    Coeficiente de correlación

c)    Prueba de Hipótesis sobre el coeficiente

d)    El modelo de regresión lineal

e)    La tensión arterial esperada para una persona de 36 años

PRUEBA DE HIPÓTESIS PARA EL COEFICIENTE DE CORRELACIÓN LINEAL

COEFICIENTE DE CORRELACIÓN

 

Definición: Grupo de técnicas para medir la asociación entre dos variables

En este tema el foco de interés cambia hacia el estudio de la relación entre dos variables, por ejemplo:

a) cantidad que se gasta por mes en publicidad y el resultado de sus ventas mensuales

b) kilómetros por litro y el peso del auto

c) relación entre el número de horas que estudiaron los alumnos para un examen y la calificación que obtuvieron

Identificando si la relación entre dos variables es:

·         Fuerte o débil

·         Directa o Inversa

Desarrollando una ecuación para expresar dicha relación y estimar una variable con base en otra, utilizando el análisis de regresión.

La idea básica del análisis de correlación es reportar la asociación entre dos variables. Por lo general, el primer paso es trazar los datos en un diagrama de dispersión.

En este diagrama debemos identificar dos variables:

·         La variable independiente proporciona la base para la estimación. Es la variable predictora. Regularmente (x)  

La variable dependiente es la variable que se desea predecir o estimar. También puede ser descrita como el resultado de un valor conocido de la variable independiente. 

Regularmente (y)

El primer paso para realizar un análisis de correlación consiste en trazar un diagrama de dispersión, determinando cuál es la variable independiente (X) y cuál la variable dependiente (Y). 

       

 2.

ANOVA

TEMA: ANÁLISIS DE VARIANZA

SUBTEMA: PRUEBA F ANOVA (Análisis de la Técnica de la Varianza)

Se trata de realizar una prueba de hipótesis para comparar tres o más medias poblacionales (m), para determinar si pueden ser iguales. Se utiliza la distribución de probabilidad  F.

Características

1. Las poblaciones siguen una distribución normal

2. Las poblaciones tienen desviaciones estándares iguales (s)

3. Las poblaciones son independientes

Ejercicios

1. Las aerolíneas desde hace algún tiempo han reducido sus servicios como alimentos y bocadillos durante sus vuelos, y empezaron a cobrar un precio adicional por algunos de ellos. Una empresa realizó una encuesta de 25 preguntas con 4 posibles respuestas: para excelente se consideraron 4 puntos, para bueno 3, para regular 2 y para deficiente 1. La calificación mayor será de 100 puntos.

De acuerdo a los siguientes valores obtenidos al encuestar pasajeros de 4 aerolíneas. ¿Hay alguna diferencia entre los niveles de satisfacción medios con respecto a las 4 aerolíneas? Use un nivel de significancia de 0.01

Northern	WTA	Pocono	Branson
94	75	70	68
90	68	73	70
85	77	76	72
80	83	78	65
	88	80	74
		68
		65

2. Se quiere evaluar la eficacia de distintas dosis de un fármaco contra la hipertensión arterial, comparándola con la de una dieta sin sal. Para ello se seleccionan al azar 25 hipertensos y se distribuyen aleatoriamente en 5 grupos. Al primero de ellos no se le suministra ningún tratamiento, al segundo una dieta con un contenido pobre en sal, al tercero una dieta sin sal, al cuarto el fármaco a una dosis determinada y al quinto el mismo fármaco a otra dosis. Las presiones arteriales sistólicas de los 25 sujetos al finalizar los tratamientos son:

Grupo
1	2	3	4	5
180	172	163	158	147
173	158	170	146	152
175	167	158	160	143
182	160	162	171	155
181	175	170	155	160

Hay diferencia significativa de la eficacia del tratamiento contra la hipertensión,  entre los cinco grupos?

3 Para determinar si existe diferencia significativa en el nivel de Matemáticas de 4 grupos de estudiantes  de Ingeniería   se realizó un examen aleatorio a 6 individuos por grupo. Determine cuáles son los grupos en los cuales existen diferencias a un 95% de nivel de confianza.

A	B	C	D
75	78	55	64
93	91	66	72
78	97	49	68
71	82	64	77
63	85	70	56
76	77	68	95